728x90
반응형
[깊이 우선 탐색 DFS]은 그래프 완전 탐색 기법 중 하나로 그래프의 시작 노드에서 출발해 탐색할 한 쪽 분기를 정해 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동해 다시 탐색하는 알고리즘이다.
깊이 우선 탐색은 실제 구현 시 재귀 함수를 이용하므로 스택 오버플로를 유의해야 한다!
깊이 우선 탐색은 단절점 찾기, 사이클 찾기, 위상 정렬 등에 응용하여 문제를 풀 수 있다.
깊이 우선 탐색의 핵심 이론
DFS는 한 번 방문한 노드를 다시 방문하면 안 되므로 노드 방문 여부를 체크할 배열이 필요하며, 그래프는 인접 리스트로 표현하겠다. 그리고 DFS의 탐색 방식은 후입선출 특성을 가지므로 스택을 사용하여 설명하겠다.
1.DFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기
원본 그래프를 인접리스트로 표현해본다. 만약 1에서 2 방문, 2에서 1 방문과 같이 서로를 방문할 수 있는 경우에는 두 가지 모두 인접리스트를 그려주어야 한다. 방문 배열은 코딩 스타일에 맞춰 int, boolean 등으로 나타낼 수도 있다.
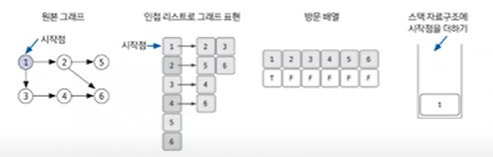
2. 스택에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 스택에 삽입한다.
3. 스택 자료 구조에 값이 없을 때까지 반복한다.
이때, 이미 다녀간 노드는 방문 배열을 바탕으로 재삽입하지 않는다.

이때 1번과 인접한 노드인 2,3 을 스택에 넣을 때, 2와 3의 넣는 순서는 중요하지 않다.
적용 코드
/**
* DFS 깊이탐색
* 백준 11724
*/
public class 연결요소_개수_구하기 {
static boolean visited[];
static ArrayList<Integer>[] a;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); //노드 개수
int m = Integer.parseInt(st.nextToken()); //에지의 개수
int result = 0;
//방문 리스트
visited = new boolean[n+1]; // 0번 인덱스는 헷갈리니 사용 안 하겠음!
//인접 리스트
a = new ArrayList[n+1];
for (int i = 1; i<n+1; i++) {
a[i] = new ArrayList<Integer>(); // 이동가능한 노드를 넣을 리스트
}
for (int i = 0; i<m; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
//방향성이 없기 때문에.
a[start].add(end);
a[end].add(start);
}
for (int i = 1; i<n+1; i++) {
if(!visited[i]) {
result++;
DFS(i);
}
}
System.out.println(result);
}
private static void DFS(int v) {
if (visited[v]) {
return; //방문한 노드라면, 탐색 중지
}
visited[v] = true;
for (int i :a[v]) {
if (!visited[i]) {
DFS(i); // 재귀함수
}
}
}
}728x90
반응형
'코딩테스트' 카테고리의 다른 글
| [너비 우선 탐색 BFS] 백준 2178 (0) | 2024.02.28 |
|---|---|
| [이진 탐색] 백준 1920 (0) | 2024.02.28 |
| [삽입 정렬] & [퀵 정렬] & [병합 정렬] & [기수 정렬] (2) | 2024.02.27 |
| [선택 정렬] 백준 1427 (1) | 2024.02.27 |
| [버블 정렬] 백준 2750 (0) | 2024.02.27 |